如今,人工智能领域的发展热火朝天,大模型强大的学习和处理能力也是有目共睹。随着这些模型在编程、代码生成、自动化测试等领域展现出越来越强大的能力,一个引人深思的问题浮现出来:大模型...
前言 本文将分享DataKit迁移MySQL到openGauss的项目实战,供广大openGauss爱好者参考。 1. 下载操作系统 https://www.openeuler.org/zh/download https://support.huawei.com/enterprise/zh...
原文 How to Discuss the Undiscussables on Your Team 在团队中处理不便讨论的敏感话题可能会令人不适,但如果无视问题,它们会不知不觉地积聚起来,影响士气。本文介绍了如何识别这些问题,...

聊聊Swift中的宏 宏,Macros是一种常见的编程技术,传统的C语言中,即包含了宏功能。宏这种功能,简单来说是在代码的预编译阶段进行静态替换,是一种非运行时的特性。但是往复杂了说,宏实际...
谷歌在2017年发布Transformer架构的论文时,论文的标题是:Attention Is All You Need。重点说明了这个架构是基于注意力机制的。 一、什么是注意力机制 在深入了解Transformer的架构原理之前...

4月16日,百度举办了 Create 2024百度 AI 开发者大会,包括百度创始人、董事长兼首席执行官李彦宏在内的多位重磅嘉宾登台演讲,并与全球各地的开发者们分享了百度在 AI 领域的最新技术进展。...

关于Java异常处理的9条原则 在Java编程中,合理有效地处理异常对于保证程序的稳定性和可维护性至关重要 充分发挥异常优点,可以提高程序可读、可靠、可维护性 本文基于Effective Java 异常章...
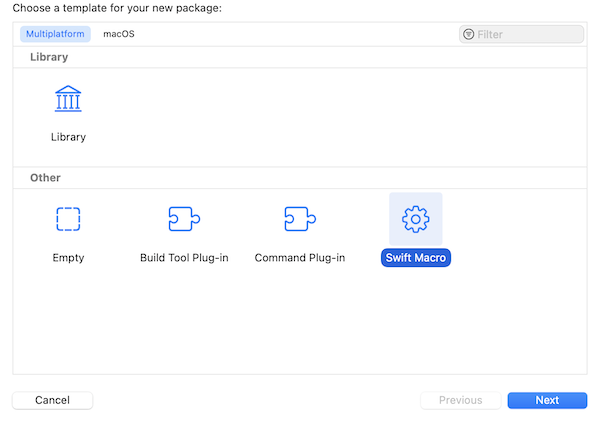
栏目介绍:“玩转OurBMC”是OurBMC社区开创的知识分享类栏目,主要聚焦于社区和BMC全栈技术相关基础知识的分享,全方位涵盖了从理论原理到实践操作的知识传递。OurBMC社区将通过“玩转OurBM...
现在,刷视频已经成为我们生活中的一部分,而且很容易一看就停不下来。你有没有好奇过,它是如何在海量的视频里,找到让你感兴趣的视频?又是如何让你可以通过关键字,搜索到与之相关的视频内...

检索增强生成(RAG)是一种新兴的 AI 技术栈,通过为大型语言模型(LLM)提供额外的“最新知识”来增强其能力。 基本的 RAG 应用包括四个关键技术组成部分: Embedding 模型:用于将外部文档...
近期,有关公共云的争议又“炸”了一把,我们在此分享一篇文章,一起来看看大佬的解读~ 作者:王小瑞,AutoMQ 联合创始人 & CEO 云计算通过资源池化实现单位资源成本更优,使企业能够将 IDC ...

Moonscript 是一门极为小众的编程语言 Moonscript 是一门编译成为 Lua 代码并在 Lua 虚拟机运行的编程语言。主要语法和特性借鉴于 Coffeescript。这门语言的优势在于语言简练、具有较强表...

01 引言 龙蜥操作系统 Anolis OS 8 是龙蜥社区(OpenAnolis)发行的开源 Linux 发行版,支持多计算架构,提供稳定、高性能、安全、可靠的操作系统支持。Anolis OS 8.9 是 Anolis OS 8 发布的...

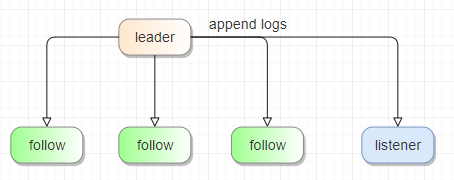
背景以及需求 线上业务对数据库可用性可靠性要求较高,要求需要有双 AZ 的主备容灾机制。 主备集群要求数据和 schema 信息实时同步,数据同步平均时延要求在 1s 之内,p99 要求在 2s 之内。 ...
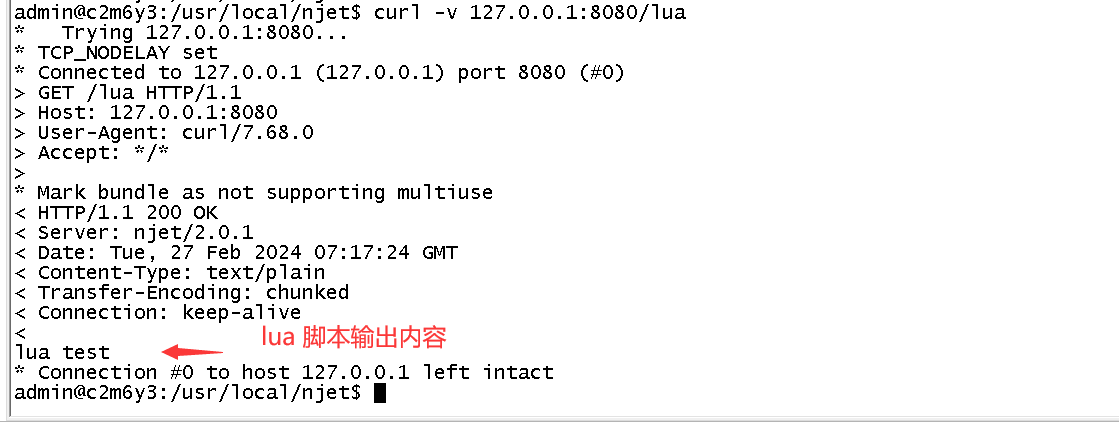
NGINX 向云原生演进,All in OpenNJet OpenNJet 是基于Nginx fork并独立演进的应用引擎,提供的Lua脚本运行能力移植自OpenResty 社区开源的lua-nginx-module 模块,该开源的Lua模块可以将Lua...
何为半连接? 半连接是在GreatSQL内部采用的一种执行子查询的方式,semi join不是语法关键字,不能像使用inner join、left join、right join这种语法关键字一样提供给用户来编写SQL语句。 两...

本文分享自华为云社区《探究数据可视化:Bokeh vs. Altair》,作者:柠檬味拥抱。 在数据科学和数据分析领域,数据可视化是一种强大的工具,可以帮助我们更好地理解数据、发现模式和趋势。P...
原文作者:NGINX 原文链接:什么是 gRPC? 转载来源:NGINX 开源社区 NGINX 唯一中文官方社区 ,尽在 nginx.org.cn gRPC(Google Remote Procedure Call,Google 远程过程调用)是一个高性能...

原文 From Zero to 50 Million Uploads per Day: Scaling Media at Canva 作为一款设计工具,Canva 吸引人的一个重要特色就是拥有数以亿计的照片和图形资源,支持用户上传个人素材。 Canva ...

熬过黑暗的 3 年 又是一个阳光明媚的春天来到了,河边的柳树已经发出嫩绿的新芽,万物都在争相复苏。 仔细算来,我这次在北京创业已经整整 3 年了,实在是不敢相信,已经熬过了这么久。 在这...